说明:本文只是一篇数学探究,与计算机图形学无关,仅考虑镜面反射,不足之处还请包涵😊。感谢Desmos为我的研究提供方便!
目录
1.1 基本概念的定义
我们知道,光子在三维空间内的运动产生人眼可见的光,我们的研究也在下图所示的三维空间中进行
三维空间中共有3条坐标轴,即x,y,z,由此我们可以引出下一节……
1.2 思路与基本公式
初中知识中一次函数解析式的求法并不适用于我们现在的研究,怎么办呢? 我们不妨来想象一个坐标系,点A的坐标为(1,1,1),点B的坐标为(2,2,2),正常人都可以一眼看出这两点在一条直线上,并且事实上三维空间中任意两点都在同一直线上。
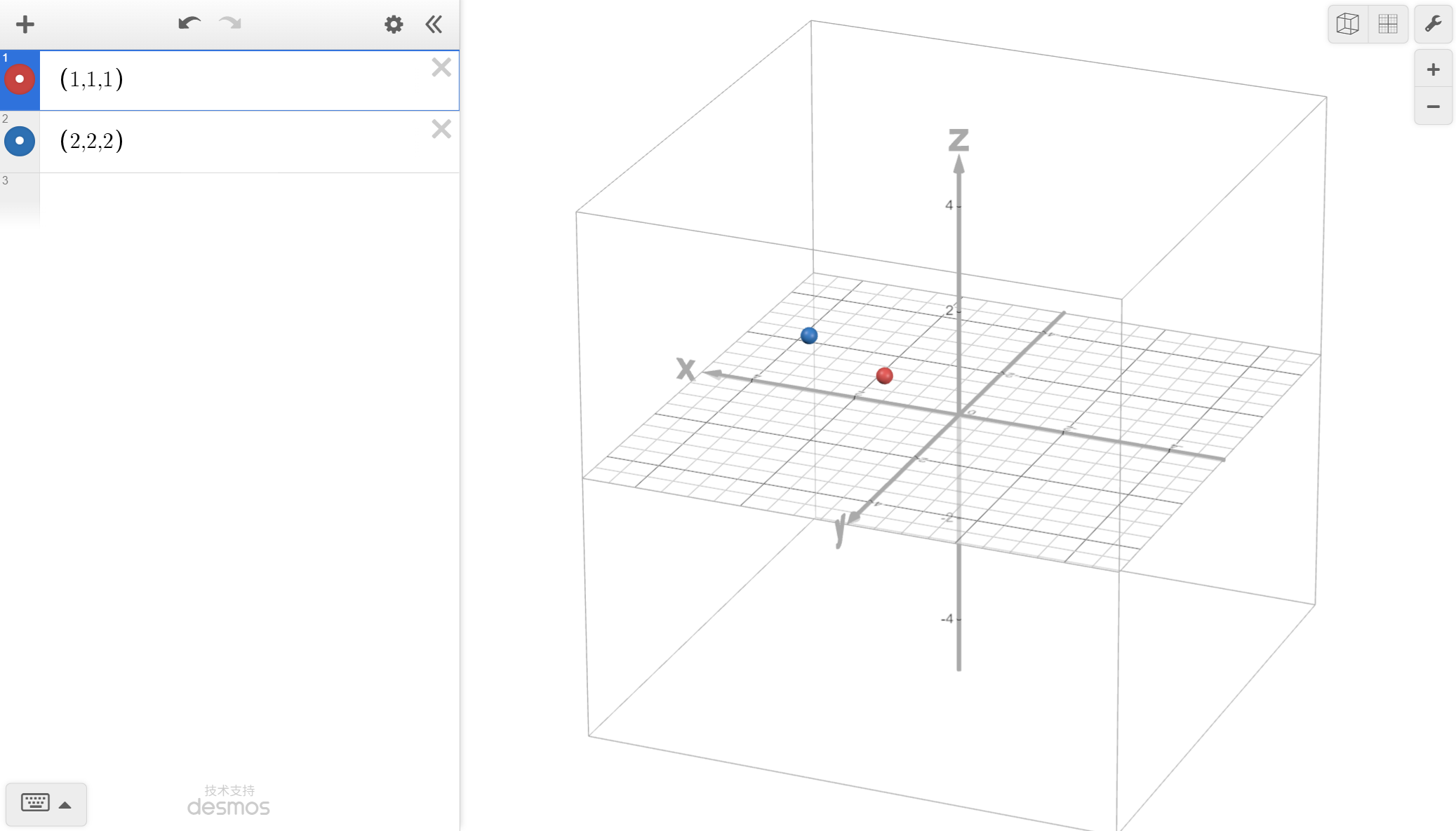
我们其实可以参考一次函数解析式的求法,用方程组来表示三维空间中的直线,还是以A,B两点为例: 我们只需分别求出A,B两点x,y坐标与x,z坐标之间的关系,如此,我们有:
设 y = kx + b</br> 1 = 1k + b</br> 2 = 2k + b</br> 可得:k = 1,b = 0</br> 则 y = x
相似地,我们求x,z之间的关系:
设 z = mx + n</br> 1 = 1m + n</br> 2 = 2m + n</br> 可得:m = 1,n = 0</br> 则 z = x
我们有了描述这条直线的方程组!
y = x</br> z = x
当然,真正的实例计算比这复杂得多,这里只是传授计算方法罢了
注:方程组还可以看出光线与坐标轴的交点位置
1.3 光线追踪初步引入
假设你有一个手电筒,你知道光线会经过一点,那么现在,你可以计算出它的路径和反射点了(如果有)!
请出我们的老朋友A点和B点,他们还在原来的位置,A点现在是手电筒,B点则是光线经过的一点,假设在y = 4的位置上有一堵墙,光线最后的落点会在哪里呢?
我先猜(4,4,4),下面就请见计算过程:
已知直线AB:y = x,z = x</br> 不难推出x = y = 4 = z</br> 故落点C的坐标为(4,4,4)
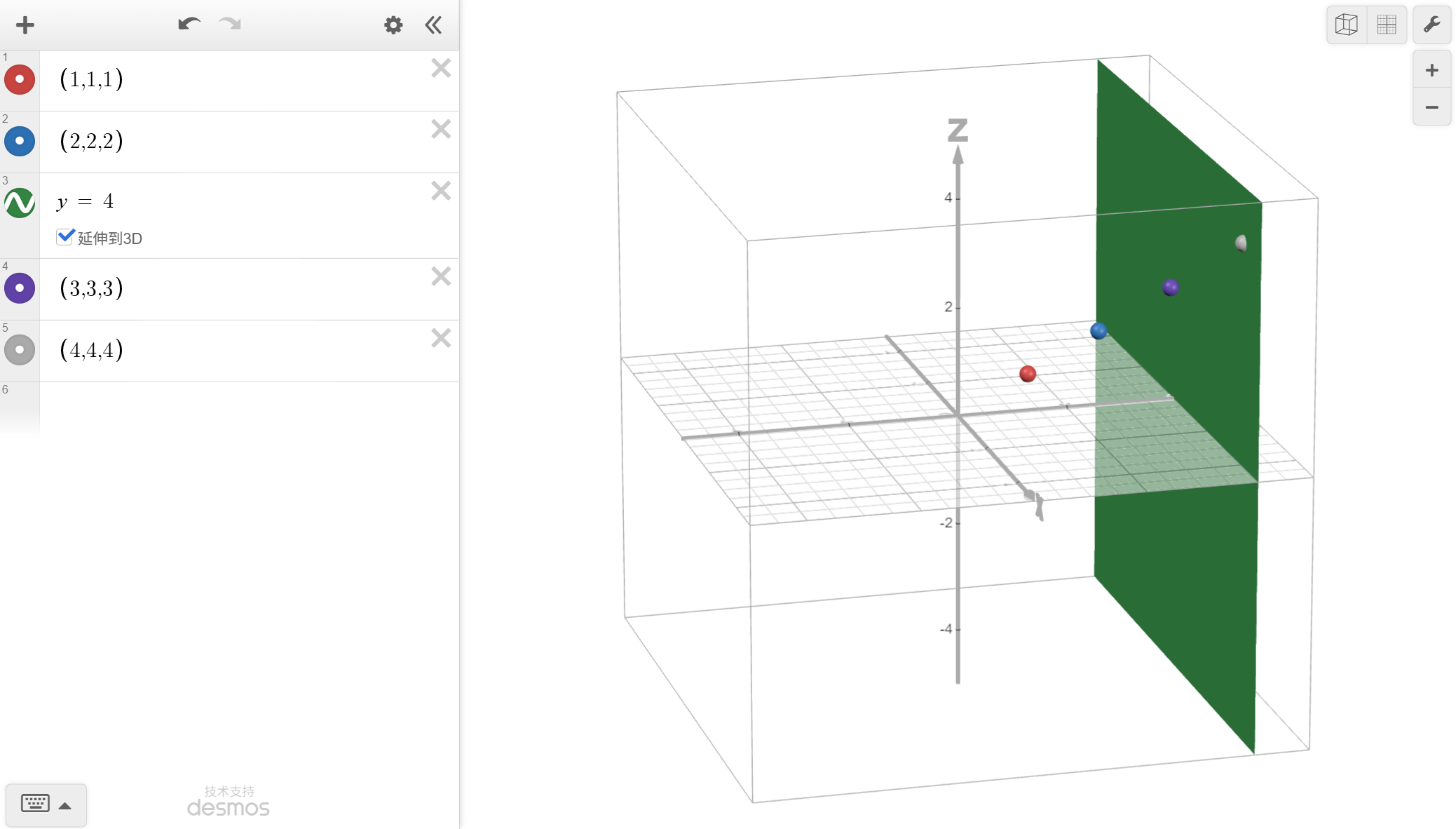
而事实也与我们的计算结果完全相符。
还有一种特殊情况,当一种坐标值无法对应唯一的另一个坐标值时,例如一个x值无法对应唯一的y值时,就应该计算光线z与y的关系。在这种情况下,一个关系式就足以表示一条光线。在下图的情况下,x值“0”对应了多个y值,所以应该计算y-z关系
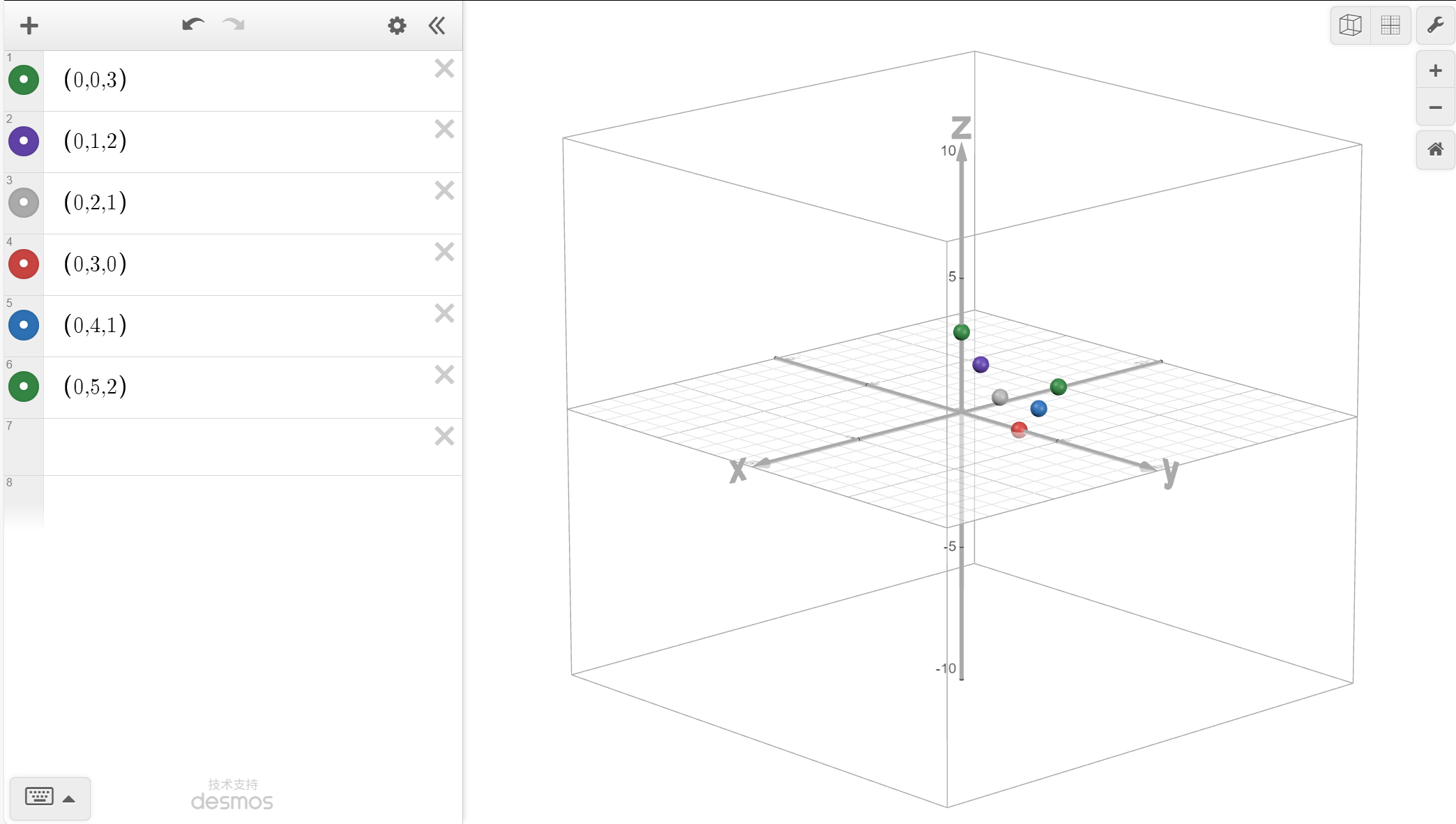
设z = cy + d</br> 3 = 0c + d</br> 2 = 1c + d</br> 可得:c = -1,d = 3</br> 则z = -y + 3</br> 验证一下,当y = 2时,z = 3-2 = 1,符合题意
2.1 平行的平面镜反射问题
现在,我们真正开始接触稍难的内容。现在,这堵位于y = 4的墙变成了平面镜,假设它绝对光滑,也就是只考虑镜面反射,光又将以什么轨迹运动呢?(等会儿再讲)
先从特殊情况入手,看到上图,光线经过反射后形成了反射光线不难看出入射,反射两条光线关于直线(0,3,-∞ < z < +∞)对称,则反射光线经过点(0,4,1)。
计算可得反射光线z = y - 3,进一步总结规律就可以得到如下公式:
z1 = cy1 + d z2 = -cy2 -d
对于一般情况,我们就不得不看到1.3节的图一,实际上笔者也不得不承认总结规律有点困难,但伟大的发现就来源于锲而不舍的努力。在这里,笔者懒得放图了,就请读者跟着我在desmos做一遍。值得注意的是,这两条光线无论何时都关于反射点(记为P)(法线)对称,并且入射光线关于y = 反射点的y值 的对称光线就是反射光线,基于这一发现,我们也可以总结出公式了。
已知P(4,4,4),入射光线一点C(1,1,1),点C关于y = 反射点y值 的对称点D(1,2yP-1,1)</br> 计算得 入射光线y = x,z = x</br> 反射光线y = -x +8,z = x
2.1.1 思路与基本公式
设入射光线y = ax + b,z = mx + n,点P(xP,yP,zP),在入射光线上随便取一点C(x,kx+b,mx+n),则点C关于yP的对称点就是D[x,yP±(yP-kx-b),mx-n],将点D和P联立即可求出反射光线解析式组。
注意!本思路仅适用于我这一场景,读者使用时要根据实际计算点D的坐标!
2.2 翻转的平面镜反射问题
本节内容至今没有想通,以下内容来自Copilot推理:
根据你的文档,2.1节讨论的是平行于坐标轴的平面镜(如 y=常数),其反射规律可以通过“关于反射点的法线对称”来推导。2.2节的“翻转的平面镜”通常指不平行于坐标轴的平面镜,比如一般的平面 Ax+By+Cz+D=0。此时,反射点的对称点和反射光线的解析式推导如下:
设平面镜方程为:
Ax + By + Cz + D = 0
其法向量为 n = (A, B, C)。
设入射光线经过点 C(x₀, y₀, z₀),方向向量为 v = (a, b, c),参数方程为:
r(t) = (x₀ + a·t, y₀ + b·t, z₀ + c·t)
将光线方程代入平面方程,解t得交点P的坐标。
点C关于平面的对称点D的坐标公式为:
D = C - 2·[(AC + BC + CC + D) / (A² + B² + C²)]·n
其中,(AC + BC + CC + D) 实际是把C的坐标代入平面方程。
反射光线的方向向量为:
v’ = v - 2·(v·n) / (±n)² · n
即入射方向关于法向量的对称。反射光线经过P,方向为v’,参数方程为:
r’(s) = P + v’·s
2.2.1 备注
1.这种推导适用于任意方向的平面镜(即“翻转的平面镜”)。
2.你可以用向量法则和参数方程直接写出反射光线的解析式。
3.不会的可以炫一包魔芋爽,虽然没用,但是爽